This took some doing, and if you ever read this Manfred, thank you for explaining some of these things to me, I'm sure there is plenty more to learn about it.
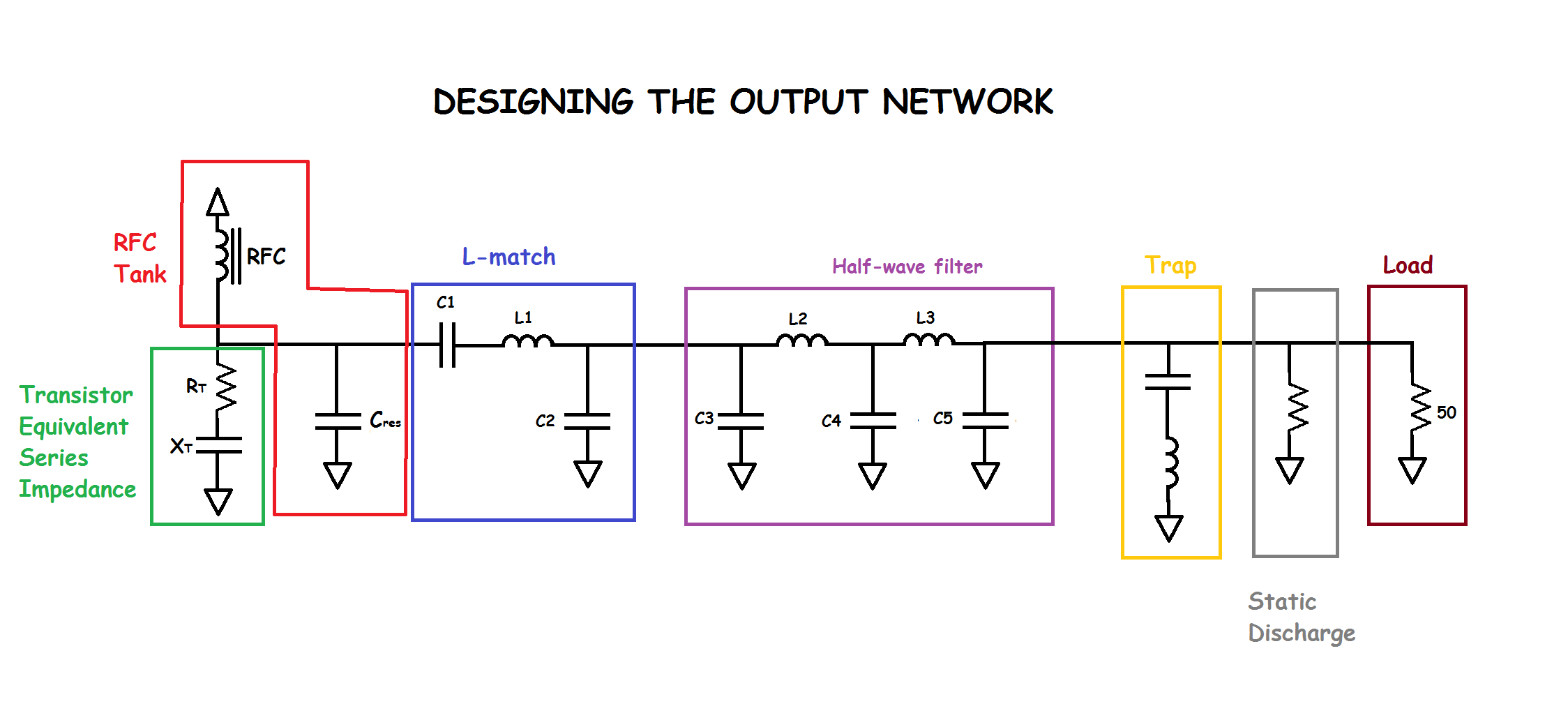
When designing the output network, the most important thing to know is the transistor’s series equivalent output impedance. If you don’t have a datasheet or it isn’t listed, you can approximate the output impedance with the formula below. By the end of this, you should have a fairly good idea how to compensate for the transistor capacitance afterward if you do not have that information at hand (it’s easy).
Formula to approximate transistor output resistance:
RL = (VCC-VCE) ^2 / 2 * PO
VCC is the collector voltage (AM dead key is half the supply), VCE is the voltage across the transistor at saturation, typically 0.5v, and PO is power in watts. Example: If you have 6.5v on the collector during AM, your VCE drop is 0.5V the radio outputs 4 watts, the transistor resistance RT is approximately 4.5, Ok, you have a transistor with a known equivalent series impedance (or at least a rough estimate of its resistance). It will need to get its power through a RFC.
The first thing to do is to decide whether or not to resonate the choke with the transistor capacitance (the parallel equivalent of the series value in the datasheet) and CRES, or, to resonate the RFC with CRES alone and use the matching network’s inductor to tune out the transistor’s capacitance. CB manufacturers choose to not resonate the choke with the transistor because doing so raises the Q of the circuit, and in a case like this where we are transforming such a low impedance (2-6Ω) to 50Ω, the ratio of those impedances forces the Q of the matching network to be high enough as is. By not resonating the RFC with the transistor, further increases to Q due to the transistor capacitance are avoided.
And that also makes variations in the choke inductance and CRES quite tolerable (but there is a limit, which I will get to). If the choke was resonated with the transistor capacitance, variations in the values of choke inductance and CRES will have a much greater effect on the overall network. Tuning out the capacitance using the L-match allows for a choke value that can almost have its decimal place moved without significant consequence to the matching network. This is due to its high parallel equivalent reactance with respect to its surroundings. But don’t make the inductance too high, because as that goes up, the chokes resonant frequency drops and that can be an issue if the transistor has a higher gain. That said, with the higher reactance of the choke, its effect can be easily compensated for in the L-network. In the case of the 2sc1969, the transistor’s parallel equivalent output capacitance is relatively large with respect to CRES, and therefore, small variations CRES are also well tolerated.
The next thing in line is the L-match. The method of designing it will depend on the choice you made at the beginning about how you resonate the RFC. Since you probably went with tuning the transistors capacitance out with L1 instead of the RFC, I will focus on that method (however, the attached excel calc does it both ways utilizing the same network layout). Keep in mind that there are countless ways to do this, each having their own advantages and disadvantages. But I’m sticking with the Cobra 148GTL here and I will avoid all of the L-match theory easily found on the web.
The reactance of C1, L1 and C2 are found as follows. The red text is the compensation for the transistor capacitance (its equivalent series value):
XC1 = Q * RT
XL1 = SQRT (RT * 50Ω – RT^2) + XC1 – XT
XC2 = RT * 50Ω / (XL1-XC1)
These formulas assume that the input of the half-wave filter is 50Ω.
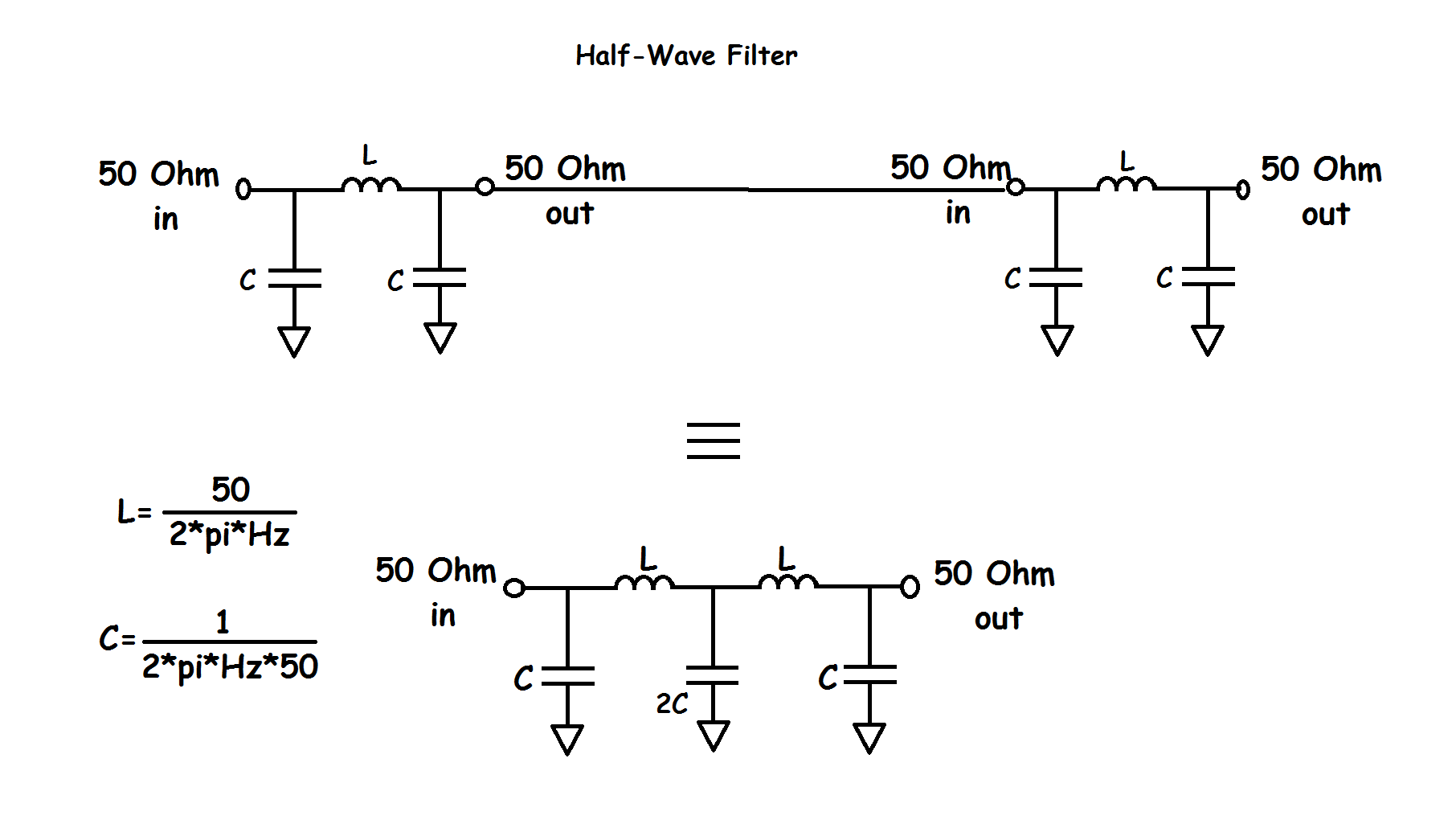
This is called a half-wave filter because it shifts the signal phase by 180°. You don’t need to understand phases and degrees and all that to build a filter. It is just two PI filters stuck back to back and the two shunt capacitors in the middle are combined into one. And since capacitances in parallel add, that’s simple math. This method of making a filter is found in Lou Franklin's book and elsewhere online.
These formulas provide values of 117pF for C and 293nH for L at 27.2MHz. These are slightly different than those used in the radio, but these model better IMO. I have a feeling these schematic values were based on a filter design table that uses normalized values, I doubt they had anything like SimSmith.
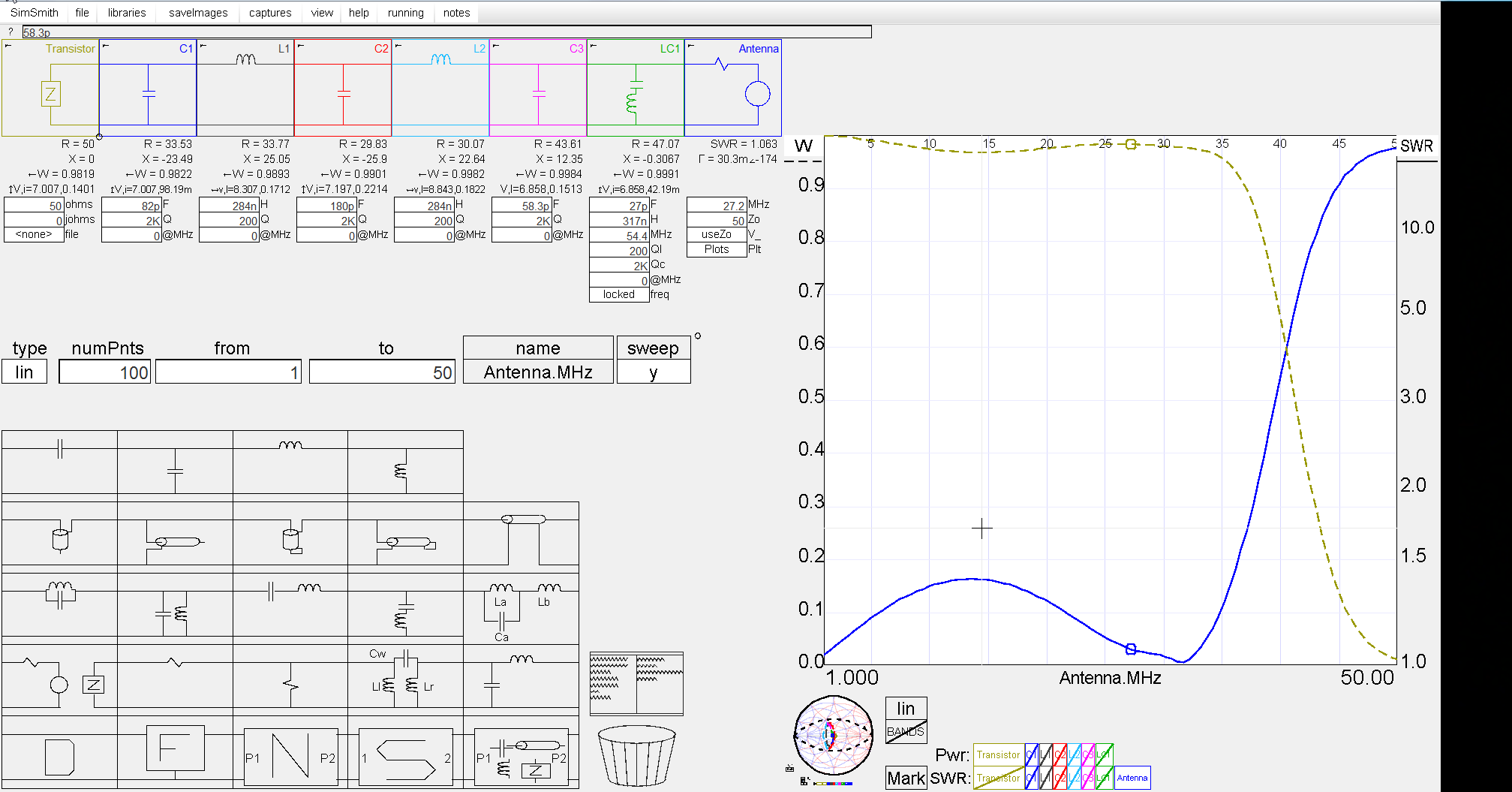
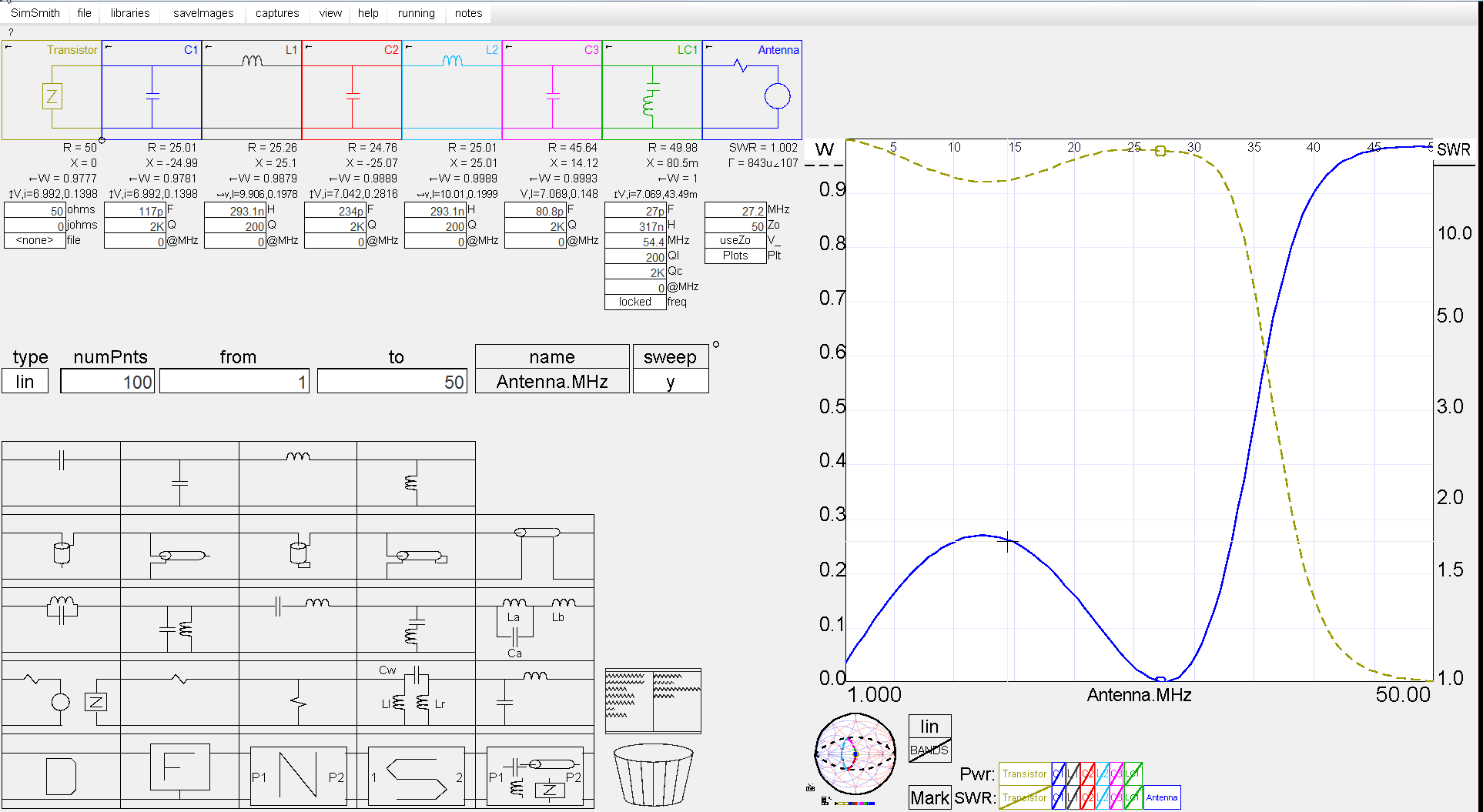
Here are two SimSmith screenshots. This is just the half-wave filter section, no L-match, and the filter cap nearest the trap has been adjusted to account for the effects of the trap in both (- about 37pF compared to the other side). The top one uses the parts from the Cobra and the bottom is using the values obtained with the filter design above. The blue trace is the SWR at the antenna jack and the green line is the power in the transistor, swept from 1MHz to 50MHz, with the small circle on the traces indicating 27.2MJz.
The trap is a series resonant circuit at 54MHz, but its presence has an effect that makes the last filter cap too large by about 37pF compared to the calculated values. The usual values for the harmonic trap are 27pF and 317nH. Make it any wider by raising the cap/lowering the coil and it will start cutting down on the fundamental as its response widens. Best to stick to those values. And don’t forget about that static discharge resistor. If you have an antenna that lacks DC ground, it is vital! And don't skip the trap thinking the filter is enough. That filter will only reduce the 2nd harmonic by about 35dB and the third 55dB. The FCC demands -60dBc and the trap helps get us there. But that don't mean the trap needs to make up a 25dB difference, unless of course your 2nd harmonic is the same strength as the fundamental.
Remember back when we had a choice to resonate the RFC with the transistor, but couldn't because the L-match already has a high Q... What matching network doesn't have a high Q? A transformer! In those situations, it is that tank which controls the BW and removes distortion. This is how those big boxes do it! Without that Q being just right, your waveform is UGLY!
As for the excel program…
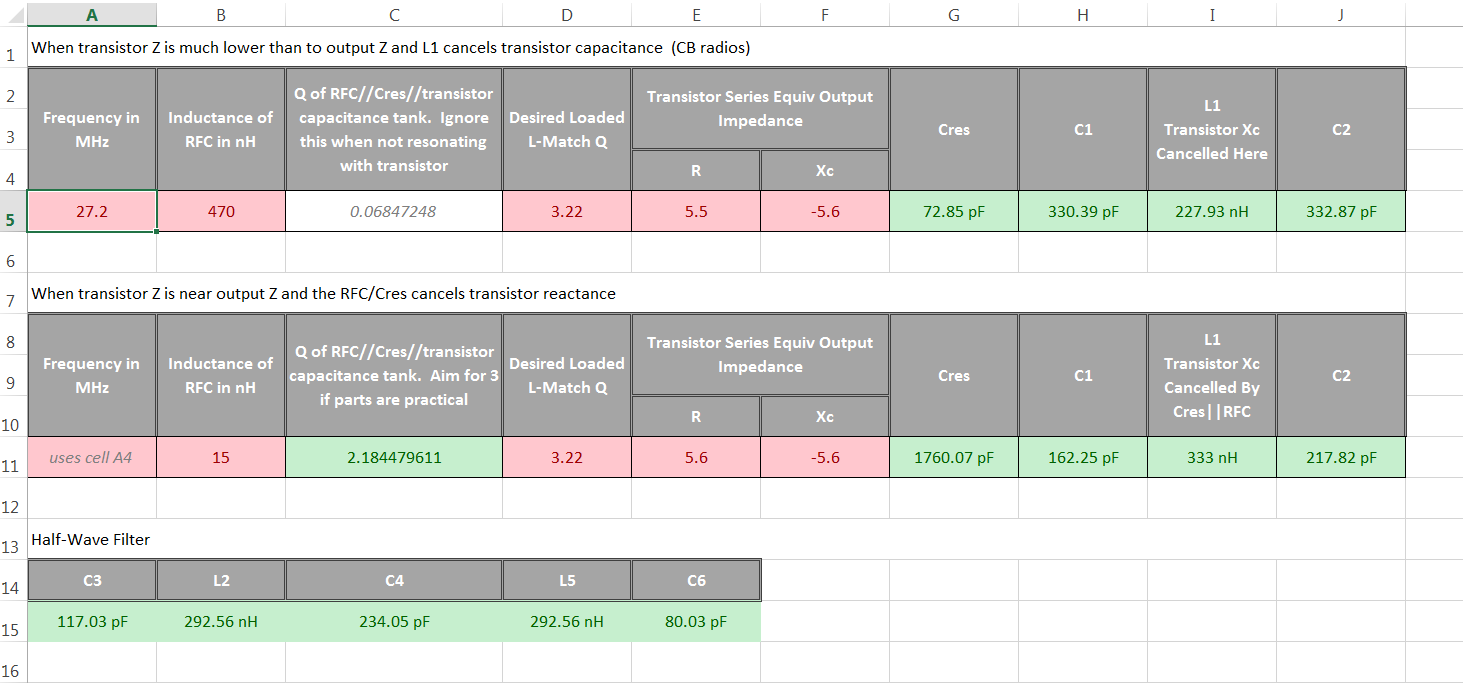
Enter data in the red boxes, get results in the green boxes. The green boxes are protected, but not with a pw. Feel free to tear it apart. The formulas in my excel calculator are the result of going back and forth between capacitance or inductance and their reactances, series/parallel conversions, combining formulas from many cascaded cells into one, etc. I did not go back and clean up the equations. I assume you have at least a Pentium II and it can probably handle a little bit of redundant math. If you want simplified formulas in excel, you gotta do that for yourself.
Edit: If the transistor reactance is 0 or all you have is a resistance, put in a small value like .01 to avoid a divide by 0 error. Maybe v2 will use excels complex number functions, I was lazy and tired. Regardless, it agrees with simsmith. It works. And be sure to put capacitive reactance in as a negative! A screenshot of the excel calc:
When designing the output network, the most important thing to know is the transistor’s series equivalent output impedance. If you don’t have a datasheet or it isn’t listed, you can approximate the output impedance with the formula below. By the end of this, you should have a fairly good idea how to compensate for the transistor capacitance afterward if you do not have that information at hand (it’s easy).
Formula to approximate transistor output resistance:
RL = (VCC-VCE) ^2 / 2 * PO
VCC is the collector voltage (AM dead key is half the supply), VCE is the voltage across the transistor at saturation, typically 0.5v, and PO is power in watts. Example: If you have 6.5v on the collector during AM, your VCE drop is 0.5V the radio outputs 4 watts, the transistor resistance RT is approximately 4.5, Ok, you have a transistor with a known equivalent series impedance (or at least a rough estimate of its resistance). It will need to get its power through a RFC.
The first thing to do is to decide whether or not to resonate the choke with the transistor capacitance (the parallel equivalent of the series value in the datasheet) and CRES, or, to resonate the RFC with CRES alone and use the matching network’s inductor to tune out the transistor’s capacitance. CB manufacturers choose to not resonate the choke with the transistor because doing so raises the Q of the circuit, and in a case like this where we are transforming such a low impedance (2-6Ω) to 50Ω, the ratio of those impedances forces the Q of the matching network to be high enough as is. By not resonating the RFC with the transistor, further increases to Q due to the transistor capacitance are avoided.
And that also makes variations in the choke inductance and CRES quite tolerable (but there is a limit, which I will get to). If the choke was resonated with the transistor capacitance, variations in the values of choke inductance and CRES will have a much greater effect on the overall network. Tuning out the capacitance using the L-match allows for a choke value that can almost have its decimal place moved without significant consequence to the matching network. This is due to its high parallel equivalent reactance with respect to its surroundings. But don’t make the inductance too high, because as that goes up, the chokes resonant frequency drops and that can be an issue if the transistor has a higher gain. That said, with the higher reactance of the choke, its effect can be easily compensated for in the L-network. In the case of the 2sc1969, the transistor’s parallel equivalent output capacitance is relatively large with respect to CRES, and therefore, small variations CRES are also well tolerated.
The next thing in line is the L-match. The method of designing it will depend on the choice you made at the beginning about how you resonate the RFC. Since you probably went with tuning the transistors capacitance out with L1 instead of the RFC, I will focus on that method (however, the attached excel calc does it both ways utilizing the same network layout). Keep in mind that there are countless ways to do this, each having their own advantages and disadvantages. But I’m sticking with the Cobra 148GTL here and I will avoid all of the L-match theory easily found on the web.
The reactance of C1, L1 and C2 are found as follows. The red text is the compensation for the transistor capacitance (its equivalent series value):
XC1 = Q * RT
XL1 = SQRT (RT * 50Ω – RT^2) + XC1 – XT
XC2 = RT * 50Ω / (XL1-XC1)
These formulas assume that the input of the half-wave filter is 50Ω.
This is called a half-wave filter because it shifts the signal phase by 180°. You don’t need to understand phases and degrees and all that to build a filter. It is just two PI filters stuck back to back and the two shunt capacitors in the middle are combined into one. And since capacitances in parallel add, that’s simple math. This method of making a filter is found in Lou Franklin's book and elsewhere online.
These formulas provide values of 117pF for C and 293nH for L at 27.2MHz. These are slightly different than those used in the radio, but these model better IMO. I have a feeling these schematic values were based on a filter design table that uses normalized values, I doubt they had anything like SimSmith.
Here are two SimSmith screenshots. This is just the half-wave filter section, no L-match, and the filter cap nearest the trap has been adjusted to account for the effects of the trap in both (- about 37pF compared to the other side). The top one uses the parts from the Cobra and the bottom is using the values obtained with the filter design above. The blue trace is the SWR at the antenna jack and the green line is the power in the transistor, swept from 1MHz to 50MHz, with the small circle on the traces indicating 27.2MJz.
The trap is a series resonant circuit at 54MHz, but its presence has an effect that makes the last filter cap too large by about 37pF compared to the calculated values. The usual values for the harmonic trap are 27pF and 317nH. Make it any wider by raising the cap/lowering the coil and it will start cutting down on the fundamental as its response widens. Best to stick to those values. And don’t forget about that static discharge resistor. If you have an antenna that lacks DC ground, it is vital! And don't skip the trap thinking the filter is enough. That filter will only reduce the 2nd harmonic by about 35dB and the third 55dB. The FCC demands -60dBc and the trap helps get us there. But that don't mean the trap needs to make up a 25dB difference, unless of course your 2nd harmonic is the same strength as the fundamental.
Remember back when we had a choice to resonate the RFC with the transistor, but couldn't because the L-match already has a high Q... What matching network doesn't have a high Q? A transformer! In those situations, it is that tank which controls the BW and removes distortion. This is how those big boxes do it! Without that Q being just right, your waveform is UGLY!
As for the excel program…
Enter data in the red boxes, get results in the green boxes. The green boxes are protected, but not with a pw. Feel free to tear it apart. The formulas in my excel calculator are the result of going back and forth between capacitance or inductance and their reactances, series/parallel conversions, combining formulas from many cascaded cells into one, etc. I did not go back and clean up the equations. I assume you have at least a Pentium II and it can probably handle a little bit of redundant math. If you want simplified formulas in excel, you gotta do that for yourself.
Edit: If the transistor reactance is 0 or all you have is a resistance, put in a small value like .01 to avoid a divide by 0 error. Maybe v2 will use excels complex number functions, I was lazy and tired. Regardless, it agrees with simsmith. It works. And be sure to put capacitive reactance in as a negative! A screenshot of the excel calc:
Attachments
Last edited:

