On common emitter push-pull transistor amplifiers there are capacitors employed from the collectors of the power transistors to ground on most amplifiers. They are usually soldered right at the output transformer. They range from 100pF to around 330pF. What is the purpose of these transistors? What effect do they have?
-
You can now help support WorldwideDX when you shop on Amazon at no additional cost to you! Simply follow this Shop on Amazon link first and a portion of any purchase is sent to WorldwideDX to help with site costs.
Transistor push-pull common emitter amplifier capacitors on collectors
- Thread starter Smiley429
- Start date
Lots of good info on the subject >>>here<<<.
Last edited:
I skimmed over that page, this is what I gathered about that particular capacitor.
That capacitor to ground is in parallel with the inductance of the primary (as the supply is also at RF ground), and its value is chosen to match that of the primary inductance forming a parallel tank (while accounting for the added capacitance of the transistor, so in reality the capacitance needed will be a little lower than suggested by the inductive reactance). This parallel tank makes the waveform at the collector sinusoidal. The Q of the tank should ideally be about 3 to achieve a balance between bandwidth and distortion (higher Q makes it really narrowband and lower Q means you don't get a nice sine wave). This suggests that the inductive reactance and capacitive reactance should be in the neighborhood of 1/3 the load impedance. On that side, the load impedance is single digit, so these reactance values will also be in the single digits.
The article gets into what happens when 1/3 of such a low impedance makes choosing parts impractical and the tradeoffs of lowering Q to make it work. It gets into DC saturation, compensation of leakage inductance as frequencies go up (the cap across the windings) and all sorts of good stuff I had no idea about!!!
That capacitor to ground is in parallel with the inductance of the primary (as the supply is also at RF ground), and its value is chosen to match that of the primary inductance forming a parallel tank (while accounting for the added capacitance of the transistor, so in reality the capacitance needed will be a little lower than suggested by the inductive reactance). This parallel tank makes the waveform at the collector sinusoidal. The Q of the tank should ideally be about 3 to achieve a balance between bandwidth and distortion (higher Q makes it really narrowband and lower Q means you don't get a nice sine wave). This suggests that the inductive reactance and capacitive reactance should be in the neighborhood of 1/3 the load impedance. On that side, the load impedance is single digit, so these reactance values will also be in the single digits.
The article gets into what happens when 1/3 of such a low impedance makes choosing parts impractical and the tradeoffs of lowering Q to make it work. It gets into DC saturation, compensation of leakage inductance as frequencies go up (the cap across the windings) and all sorts of good stuff I had no idea about!!!
I thought it would be fun to try doing the math on one of these capacitors. Lets go with the old-school 2879 because it had a useful datasheet.
First of all, we have a primary (the tube that goes through the core), and, not discussing all the other transformer design factors I don't yet understand, lets say that primary ends up having a reactance of 2.6Ω. The circuit looks like this, and because the rail is at RF ground, the primary is in parallel with C. Our job is to determine what C should be based on the measured inductance of the primary (remember, we want resonance here) accounting for the capacitance of the transistor.
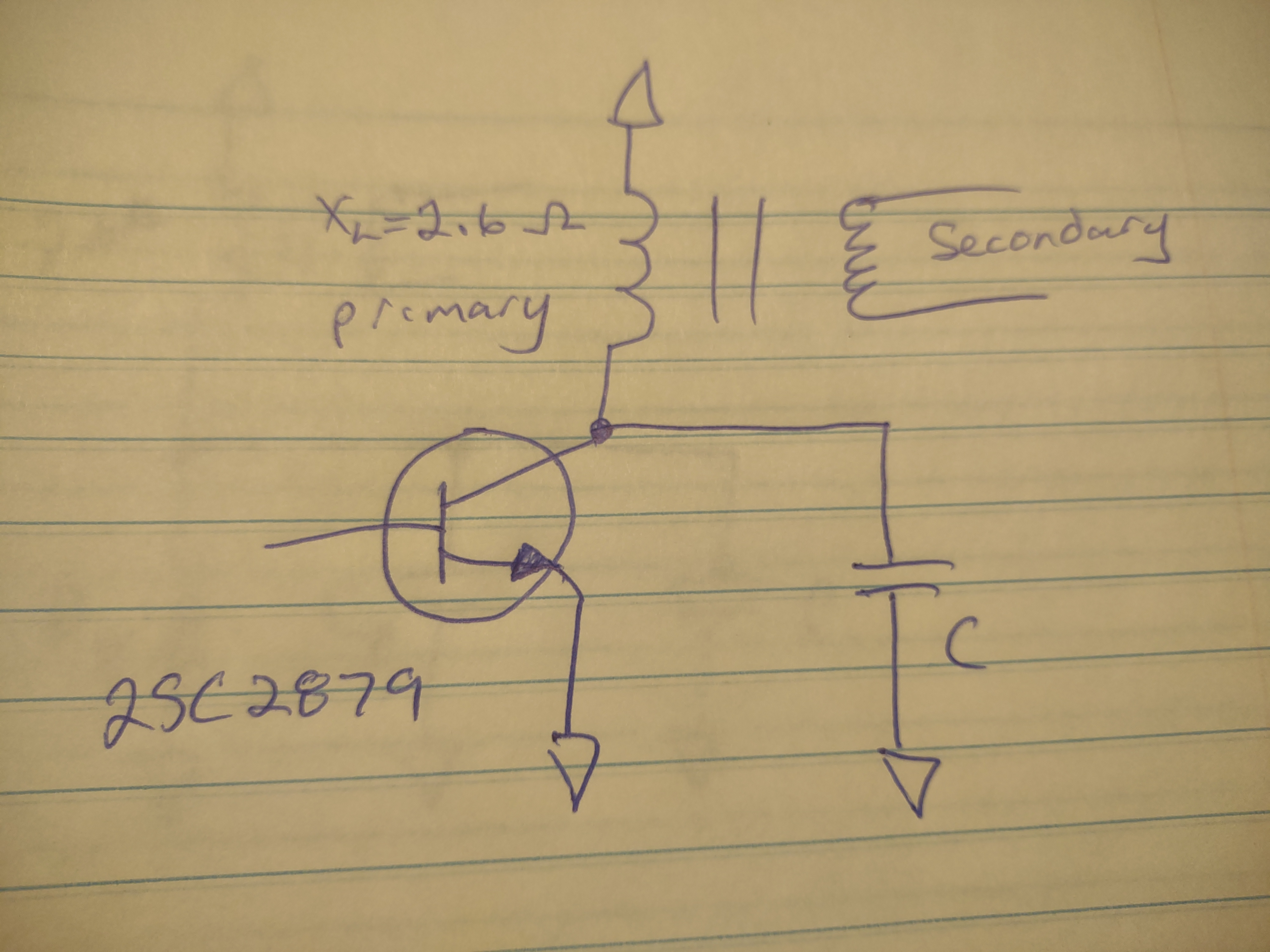
First thing we do is look at the datasheet to get the series equivalent output impedance. For the 2SC2879, it is listed as 1.45-j1. So, replacing the transistor with it's equivalent, we get this, where Rs is 1.45Ω and Xs is 1Ω @11m (Cs=5.85nF):
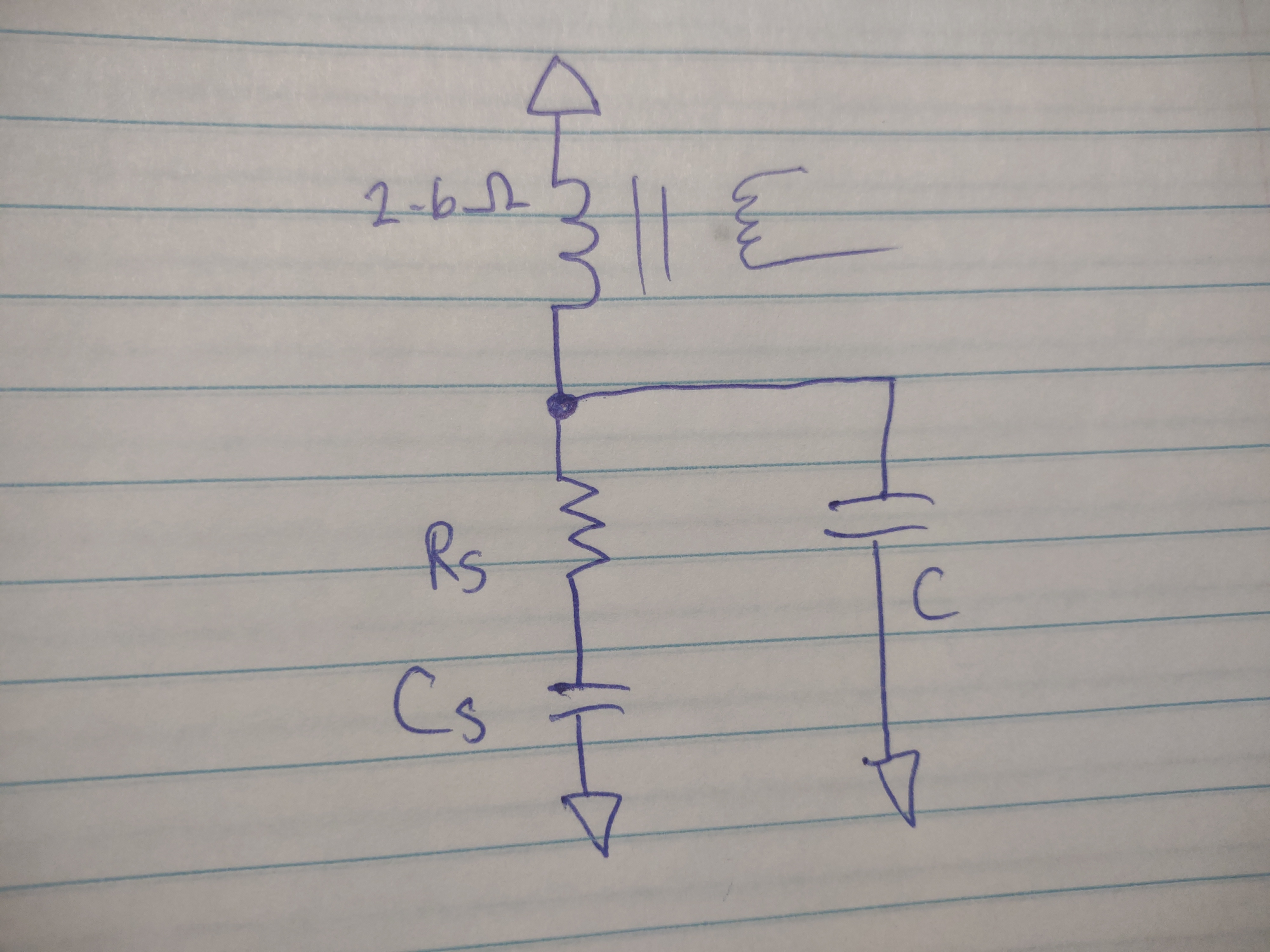
But before we can figure out C, we need to make Rs and Cs into their parallel equivalents so that we can combine the capacitances. Now it looks like this, with Rp = 4.5Ω and Xp = 3.1Ω (1.89nF)
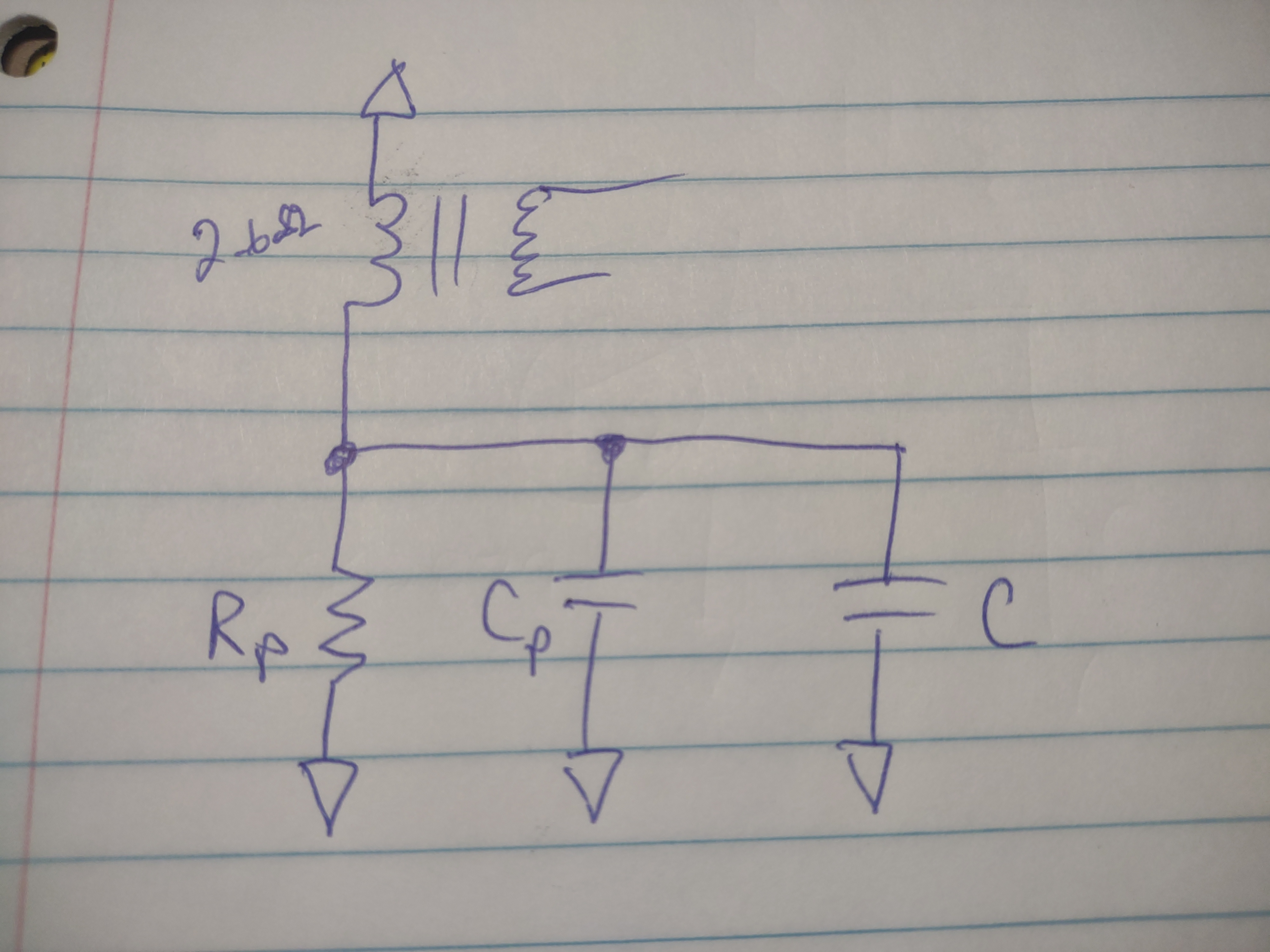
So, if we know the total capacitance must have a reactance of 2.6Ω, the total capacitance must be 2.25nF. How much capacitance must be added to 1.89nF to make it 2.25nF? 360pF. C = 360pF
First of all, we have a primary (the tube that goes through the core), and, not discussing all the other transformer design factors I don't yet understand, lets say that primary ends up having a reactance of 2.6Ω. The circuit looks like this, and because the rail is at RF ground, the primary is in parallel with C. Our job is to determine what C should be based on the measured inductance of the primary (remember, we want resonance here) accounting for the capacitance of the transistor.
First thing we do is look at the datasheet to get the series equivalent output impedance. For the 2SC2879, it is listed as 1.45-j1. So, replacing the transistor with it's equivalent, we get this, where Rs is 1.45Ω and Xs is 1Ω @11m (Cs=5.85nF):
But before we can figure out C, we need to make Rs and Cs into their parallel equivalents so that we can combine the capacitances. Now it looks like this, with Rp = 4.5Ω and Xp = 3.1Ω (1.89nF)
So, if we know the total capacitance must have a reactance of 2.6Ω, the total capacitance must be 2.25nF. How much capacitance must be added to 1.89nF to make it 2.25nF? 360pF. C = 360pF
Shadetree Mechanic
Delaware Base Station 808
This is what ChatGPT says:
The capacitors placed from the collectors of the power transistors to ground in common emitter push-pull transistor amplifiers serve a few purposes:
1. **RF Filtering**: They help to filter out high-frequency components or RF interference that might be present in the signal. These capacitors act as a short circuit to ground for high-frequency signals, ensuring that only the desired audio or lower-frequency signals pass through the output transformer.
2. **Stability and Oscillation Prevention**: They aid in stabilizing the amplifier by preventing oscillations at higher frequencies. These capacitors prevent high-frequency oscillations that might occur due to feedback, parasitic capacitance, or unintended coupling in the circuit.
3. **DC Blocking**: They serve to block any DC component that might be present at the collector of the transistors, ensuring that only the AC signal reaches the output transformer. This is crucial in preventing DC offset issues in the output stage of the amplifier.
Their values (typically ranging from 100pF to 330pF) are chosen based on the desired frequency response and stability of the amplifier circuit.
By controlling high-frequency signals and blocking DC while allowing the desired audio frequencies to pass through to the output transformer, these capacitors contribute to maintaining the fidelity and stability of the amplified signal.
The capacitors placed from the collectors of the power transistors to ground in common emitter push-pull transistor amplifiers serve a few purposes:
1. **RF Filtering**: They help to filter out high-frequency components or RF interference that might be present in the signal. These capacitors act as a short circuit to ground for high-frequency signals, ensuring that only the desired audio or lower-frequency signals pass through the output transformer.
2. **Stability and Oscillation Prevention**: They aid in stabilizing the amplifier by preventing oscillations at higher frequencies. These capacitors prevent high-frequency oscillations that might occur due to feedback, parasitic capacitance, or unintended coupling in the circuit.
3. **DC Blocking**: They serve to block any DC component that might be present at the collector of the transistors, ensuring that only the AC signal reaches the output transformer. This is crucial in preventing DC offset issues in the output stage of the amplifier.
Their values (typically ranging from 100pF to 330pF) are chosen based on the desired frequency response and stability of the amplifier circuit.
By controlling high-frequency signals and blocking DC while allowing the desired audio frequencies to pass through to the output transformer, these capacitors contribute to maintaining the fidelity and stability of the amplified signal.